What mathematics underly fractals?

The areas of geometry, nonlinear dynamics and statistical scaling laws underly fractal structures. Described below are some key mathematical concepts.

1. Fractal Dimension (Hausdorff Dimension)

Fractal structures exist between integer dimensions. Instead of describing objects as existing in between 1,2 and 3D space, their complexity is captured as existing between in between these integer dimensions.

Fractal dimension = log(number of self-similar pieces)/log(magnification factor)

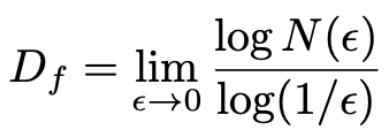
Where N(ϵ) is the number of self-similar pieces when the structure is scaled by ϵ.

ϵ is the scaling factor.

The fractal dimension for the Koch snowflake is computed as follows:

2. Box-Counting method (Empirical Fractal Dimension)

This method is used to measure the fractal dimension of real-world data, like biological structures or galaxies

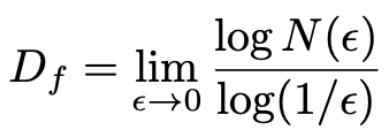
where N (ϵ) is the number of boxes of size ϵ needed to cover the object.

This formula is also used in biological systems such as neuron structures, lung patterns, blood vessel networks.

Image from the division of blood vessels in the inner half of the liver, seen from its inferior surface. Image from https://www.flickr.com/photos/133115863@N08/18700541011

Examples exist in other fields. For example, in geographical features such as coastlines and river networks.

3. Power Laws and Scaling Behaviour

   
   

Fractals obey power law distributions, which means that small elements are extremely common, while large elements are rare.

Power law formula:

Where P(x) is the probability of an event of size x. α is the scaling exponent.

Some examples in nature include:

• Earthquakes: The Gutenberg-Richter law follows a power law distribution

• Galaxies: The clustering of galaxies follows fractal statistics

• Biology: The distribution of branch sizes in trees or blood vessels follows power laws

"Galaxy Cluster Abell 1689" by NASA Goddard Photo and Video is licensed under CC BY 2.0.

4. Diffusion-Limited Aggregation (DLA)

DLA describes how fractal-like patterns emerge from random growth. It is used in:

• Snowflake formation

• Coral growth

• Electrodeposition in batteries

A particle undergoes random motion (Brownian motion) until it sticks to an existing structure, forming a fractal cluster with dimension:

Reference:

T.A. Witten & L.M. Sander, Diffusion-Limited Aggregation, Physical Review Letters (1981).

5. Murray’s Law (Optimized Transport in Fractals)

Describes how fractal branching structures in biological transport systems (blood vessels, trees, lungs) optimize flow with minimal energy loss.

Mathematical Form:

where:

• rd is the radius of the parent branch

• rd+1,rd+2 are the radii of the daughter branches

Murrays law is used in:

• Cardiovascular systems to minimize blood flow resistance

• Tree branching to optimise sap transport

Reference: C.D. Murray, "The Physiological Principle of Minimum Work," Proceedings of the National Academy of Sciences (1926).

6. Lacunarity (Texture & Gaps in Fractals)

Lacunarity measures the gaps or voids in a fractal structure. Two fractals with the same dimension can look different if they have different lacunarity.

Mathematical Definition:

where:

is the mean density at scale r

is the variance at that scale

Applications:

• Distinguishing fractal textures in medical images (e.g., tumor tissue vs. healthy tissue).

• Characterizing roughness in planetary surfaces

Reference: P. Voss, "Fractal Dimension and Lacunarity," Physica D (1988).

7. Random Fractal Models (Percolation Theory)

Fractal structures can emerge from random processes like percolation — where connectivity emerges at a critical threshold.

Mathematical Form:

where:

p is the probability of a site being occupied.

pc is the critical threshold.

is a critical exponent.

Used in:

• Forest fire models (spread of fire)

• Disease transmission networks (COVID-19 modeling)

Reference: D. Stauffer & A. Aharony, Introduction to Percolation Theory (1992).

In conclusion, fractal structures in nature arise because they optimize transport, minimize energy, and adapt dynamically. The mathematics behind them spans geometry, probability, and statistical physics, making them an exciting bridge between pure math and real-world complexity.